Problem statement
Given two strings text1 and text2, return the length of their longest common subsequence. If there is no common subsequence, return 0.
A subsequence of a string is a new string generated from the original string with some characters (can be none) deleted without changing the relative order of the remaining characters.
For example, “ace” is a subsequence of “abcde”.
A common subsequence of two strings is a subsequence that is common to both strings.
Link to problem
Example 1
Input: text1 = "abcde", text2 = "ace"
Output: 3
Explanation: The longest common subsequence is "ace" and its length is 3.
Example 2
Input: text1 = "abc", text2 = "abc"
Output: 3
Explanation: The longest common subsequence is "abc" and its length is 3.
Solutions
Approach 1: Dynamic Programming - Bottom Up
This was easier to come up with than the last problem, we essentially tabulate two strings and check for the occurences. The following picture may describe it far better than anything
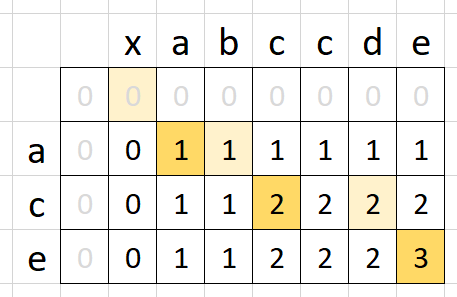
What happens is:
- Do the two characters in the table match? then that cell will be 1 + whatever the previous row and column had.
- If they do not match, take the max of left cell or the cell above, because there is a possibility that there could be continuation of the subsequence.
Pseudocode
initialize 2d array dp of size N+1 x M+1
begin ith loop from 1 to N + 1
begin jth loop from 1 to M + 1
if characters match
dp[i][j] = max of current cell or 1 + previous diagonal cell
else
dp[i][j] = max of previous row or column
return dp[N][M]
Implementation in Rust
fn longest_common_subsequence(text1: String, text2: String) -> i32 {
let mut dp = vec![vec![0; text2.len() + 1]; text1.len() + 1];
for i in 1..text1.len() + 1 {
for j in 1..text2.len() + 1 {
if text1.chars().nth(i - 1) == text2.chars().nth(j - 1) {
dp[i][j] = std::cmp::max(dp[i][j], 1 + dp[i - 1][j - 1]);
} else {
dp[i][j] = std::cmp::max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
dp[text1.len()][text2.len()]
}
Time Complexity: $O(nm)$
Space Complexity: $O(nm)$
Runtime on LeetCode: $1179$ms, that doesn’t feel optimal.
Neetcode mentioned a similar approach but his started at the end and finished at (0,0) Similar implementation but just reverse the loops.